排序算法总结

稳定排序：冒泡排序、插入排序、归并排序、基数排序

不稳定排序：选择排序、快速排序、希尔排序、堆排序

冒泡排序

总共需要比较n - 1趟，每趟n - 1 - i次。

void bubbleSort(T a[], int n) {
    for (int i = 0; i < n - 1; i++)
        for (int j = 0; j < n - 1 - i; j++)
            if (a[j] > a[j + 1]) swap(a[j], a[j + 1]);
}

快速排序

基于分治和递归。

其基本思路是，在数组中选择一个元素作为基准值，然后将数组中小于基准值的元素移动到它的左边，大于基准值的元素移动到它的右边。然后对左右两个子数组递归地重复这个过程，直到子数组的大小为1或0。

是不稳定排序。当要比较的值和基准值一样时，根据代码可能放在基准值左边或右边。

最好情况：每次划分左右两边的元素数量相同各为一半，则此时时间复杂度为O(nlogn)

最坏情况：每次划分所有元素都在一边，另一边为空，则此时与冒泡排序类似，时间复杂度为O(n²)

平均情况：时间复杂度为O(nlogn)

因此关键在于每次基准值的选取。

通过不同方式选取基准值，有以下几种衍生快排：

• 随机快速排序：即在数组中完全随机地挑选一个值作为基准值。

• 三数取中快速排序：即取数组中第一个、中间、最后一个这三个元素的中位数作为基准值。

• 三划分快速排序：适用于数组中有较多大小相同的数。对于等于基准值的数分为除左右外的第三部分，不用继续参与递归。

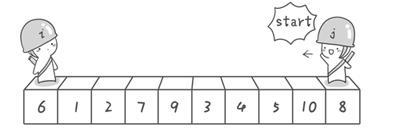
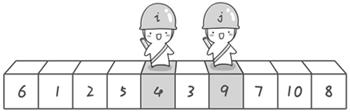
图解：

以数组中第一个元素为基准值

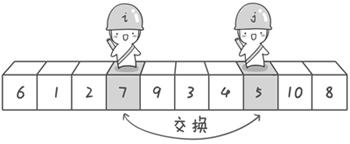
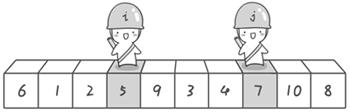
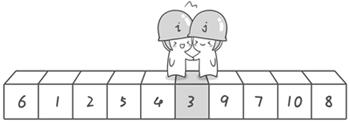
左指针不断右移，直到找到比基准值大的元素停下；右指针不断左移，直到找到比基准值小的元素停下

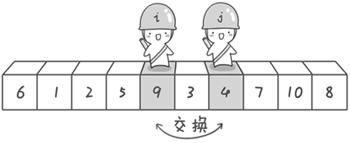
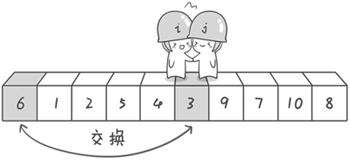
当两指针碰面或超过，说明已经全部遍历了

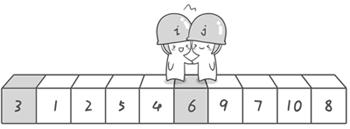
交换后左边都小于基准值，右边都大于基准值

/// 以数组中第一个元素为基准值，确定其位置
int partition(T a[], int begin, int end) {
    int left = begin + 1;
    int right = end;
    T base = a[begin];
    while (true) {
        while (a[left++] < base);   // 左指针不断右移，直到找到比基准值大的元素
        while (a[right--] > base);  // 右指针不断左移，直到找到比基准值小的元素
        if (left >= right) break;    // 当两指针碰面或超过，说明已经全部遍历了
        swap(a[left], a[right]);
    }
    swap(a[right], a[begin]);       // 交换后right左边都小于base，右边都大于base
    return right;
}

int randomPartition() {
    int randomIndex = Random(begin, end);  // 可取不同值作为基准值，这里随机一个下标
    swap(a[randomIndex], a[begin]);
    return partition(a, begin, end);
}

void quickSort(T a[], int begin, int end) {
    if (begin < end) {
        int middle = partition(a, begin, end);
        quickSort(a, begin, middle - 1);
        quickSort(a, middle + 1, end);
    }
}

堆排序

平均时间复杂度：O(nlogn)

最坏时间复杂度：O(nlogn)

public class HeapSortTest {
    /// 堆排序（大根堆）
    public int[] heapSort(int[] nums) {
        buildMaxHeap(nums);
        int heapSize = nums.length;
        for (int i = 0; i < nums.length - 1; i++) {
            // 将堆中第一个与最后一个交换
            int curr = nums[0];
            nums[0] = nums[heapSize - 1];
            nums[heapSize - 1] = curr;

            heapSize--;
            adjust(nums, heapSize, 0);
        }
        return nums;
    }

    /// 从最后一个非叶节点开始，倒着往前调整排序
    public void buildMaxHeap(int[] nums) {
        for (int i = nums.length / 2 - 1; i >= 0; i--) {
            adjust(nums, nums.length, i);
        }
    }

    /// 将下标为i的节点与其左右子节点进行比较调整，若有交换则递归地比较交换的子节点，确保交换后子树依然有序
    public void adjust(int[] nums, int heapSize, int i) {
        int l = (i + 1) * 2 - 1;
        int r = (i + 1) * 2;
        int max = i;
        if (l < heapSize && nums[l] > nums[max]) max = l;
        if (r < heapSize && nums[r] > nums[max]) max = r;
        if (i != max) {
            // 父节点与比其大的子节点交换
            int curr = nums[i];
            nums[i] = nums[max];
            nums[max] = curr;

            adjust(nums, heapSize, max);
        }
    }
}